I first wrote about the use of infinite series for the purposes of computation in my post Charles Matthew Whish Writes About Infinite Series Known to Indian Mathematicians. In Europe, one of the first to write about infinite series was John Wallis (1616-1703), who published in 1656 his Arithmetica Infinitorum (The Arithmetic of the Infinites), for which Jacqueline Stedall published in 2004 an English-language translation under the more appropriate title The Arithmetic of the Infinitesimals.1 In this book, whose ultimate result is the derivation of the infinite expression
Wallis works with the indivisibles proposed by Cavalieri and developed by Torricelli to derive the quadrature of curves of the form y = kxⁿ (using modern notation), where n is some index, not necessarily a positive integer.
For background on the indivisibles, see my previous posts
Bonaventura Cavalieri Uses Indivisibles to Calculate the Area of a Spiral
Evangelista Torricelli's Indivisibles Have Infinitesimal Thickness
In his book, Wallis introduces a notation that is today recognized by anyone today who has learnt basic mathematics: the index notation for expressing exponentiation:
A number m raised to the power 0 is always 1. Hence
2⁰ = 1
A number m raised to a positive integer n is m multiplied by itself n times. Hence
2¹ = 2
2² = 2×2 = 4
2³ = 2×2×2 = 8
2⁴ = 2×2×2×2 = 16
…
A number m raised to a negative integer -n is 1 divided n times by m. Hence
2⁻¹ = ½
2⁻² = 1/(2×2) = ¼
2⁻³ = 1/(2×2×2) = ⅛
2⁻⁴ = 1/(2×2×2×2) = ¹⁄₁₆
…
A number m raised to a positive fraction ¹⁄ₙ is the n-th root of n. Hence
2^½ = √2 (square root of 2)
2^⅓ = ∛2 (cube root of 2)
2^¼ = ∜2 (fourth root of 2)
…
A number m raised to a negative fraction ⁻¹⁄ₙ is 1 divided by the n-th root of n. Hence
2^⁻½ = 1/√2
2^⁻⅓ = 1/∛2
2^⁻¼ = 1/∜2
…
In this post, I will present quotations from Wallis’s Arithmetic of the Infinitesimals that introduce this notation, which I consider to be as important as the decimal fractions that Simon Stevin (1548-1620) presented to Europe in 1585, as I wrote in my post Simon Stevin Introduces the Arithmetic of Decimal Fractions.
Wallis’s book is a transitional point in the arithmetization of geometry. His objective is to relate (arithmetic) infinite series to (geometric) figures made up of indivisibles. He starts out very simply, with the following table
showing that the sum from 0 to m, step 1, is always half of the sum of an equal number of m. He goes further, arguing that any step can be chosen. So, below, I have taken m=8, and played with steps of 8, 4, 2, 1 and ½. They all give the same result, namely ½.
Wallis then argues that if the steps are made infinitely small, the same result will hold, and so these series can be correlated with sets of indivisibles. It follows, for example, that the quadrature of a triangle is half that of a parallelogram.
Wallis then moves on to series of squares. Here, in the numerator, squares are summed from 0² to m², and in the denominator, there is an equal number of m². The result is always greater than ⅓, although as the series grow in length, the result approaches ⅓:
Once again, the step need not be 1. So, below, I have taken m=8, and played with steps of 8, 4, 2, 1 and ½. As the series grow in length, the result approaches ⅓:
Wallis then argues that if the steps are made infinitely small, the result will be exactly ⅓. Correlating these series with sets of indivisibles, it follows, for example, that the cubature of a cone is one third of that of a cylinder.
We can continue with the same process with sums of cubes. The fractions approach ¼ as the series in the numerator and numerator grow:
Wallis generalizes these results for infinite series in Proposition 64 (Theorem, p.56). In so doing, be makes explicit the idea of integer and fractional indices to express powers and roots, exactly as I described above. When fractions with the numerator and denominator are given as series of powers of n in the example above, the sum always approaches ¹⁄ₙ₊₁:
If there is considered an infinite series, of quantities beginning from a point or 0, continually increasing according to any power either simple or composite, then the ratio of all of them, to a series of the same number of terms equal to the greatest, is that of unity to the index of that power increased by one. I set the indices of first powers, second powers, third powers, fourth powers, etc. (or laterals, squares, cubes, biquadrates, etc.) to be 1, 2, 3, 4, etc.; I set the indices of second roots, third roots, fourth roots, etc. (or square roots, cube roots, biquadratic roots, etc. of first powers, or arithmetic proportionals) to be ½, ⅓, ¼, etc. I form the composed index of any composite power from the indices of the composing powers. Thus, cubes of second powers (or squares of third powers) have index 6 = 2 × 3; cube roots of second roots (or square roots of third roots) have index ⅙ = ½ × ⅓; cubes of square roots of fifth powers will have index 15/2 = 3 × ½ × 5.
Moreover, the ratios assigned to these powers (in the tables) are of the same kind. Thus to first powers, second powers, third powers, fourth powers, etc. 1 to 2, 1 to 3, 1 to 4, 1 to 5, etc., that is 1 to 1 + 1, 1 to 2 + 1, 1 to 3 + 1, 1 to 4 + 1, etc. To second roots, third roots, fourth roots, etc., 2 to 3, 3 to 4, 4 to 5, etc. or 1 to 1½, 1 to 1⅓, 1 to 1¼, etc., that is 1 to ½ + 1, 1 to ⅓ + 1, 1 to ¼ + 1, etc. To squares of third powers (or sixth powers), 1 to 7, that is 1 to 6 + 1. To square roots of third powers, 2 to 5, or 1 to ⁵⁄₂, that is 1 to ³⁄₂ + 1. To cube roots of second roots (or sixth roots) 6 to 7, or 1 to ⁷⁄₆, that is 1 to ⅙ + 1. To cubes of square roots of fifth powers (or square roots of fifteenth powers), 2 to 17, or 1 to 17/2, that is 1 to 15/2 + 1. (And so on for the rest.) Which the theorem confirms. And if the index is supposed irrational, thus √3, the ratio will be as 1 to 1 + √3, etc.
Wallis continues on with explanations on how series can be manipulated, term by term. For example, in Proposition 73 (Theorem, pp.61-62), he explains how series can be multiplied term by term. This is where he introduces the notation of a superscript n on the surd symbol to indicate the n-th root. The only difference with today’s notation is that today the n is placed superscript-left as opposed to superscript-right.
If any two series (or also more) are multiplied term by term (that is the first term of one by the first of the other, the second by the second, etc.) there will be produced another series of the same kind, which will have an index that is the sum of the indices of the multiplied series. Moreover, its ratio to a series of terms equal to its greatest will be that which the preceding tables (or also Proposition 64) indicated.
For example, if a series of squares or second powers (with index 2) is multiplied term by term by a series of cubes or third powers (with index 3) it will produce a series of fifth powers (with index 5 = 2 + 3), which will therefore have, to a series of terms equal to the greatest, the ratio 1 to 6 (= 5 + 1). Thus if a series of second powers is multiplied term by term by a series of third powers, it will produce a series of fifth powers.
In the same way, if a series of second powers (with index 2) is multiplied term by term by a series of third roots (with index ⅓) there will be produced a series of cube roots of seventh powers (with index ⁷⁄₃ = 2 + ⅓) which, to a series of the same number of terms equal to the greatest, is as 1 to 10/3 (= ⅓ + 1), or as 3 to 10. Thus if there are multiplied term by term
In the same way, if a series of second roots (with index ½) is multiplied term by term by a series of fifth roots (with index ⅕), there will be produced a series of tenth roots of seventh powers (with index ⁷⁄₁₀ = ½ + ⅐) and therefore it will have, to a series of terms equal to the greatest, a ratio that is 1 to 17/10 (= ⁷⁄₁₀ + 1), or 10 to 17. Thus if there are multiplied term by term
And this holds similarly in other multiplications of this kind.
Similar argumentation is used for division of series term by term, and for the introduction of negative indices, corresponding to reciprocals.
It should be understood that the successful introduction of new notation allows the expression of more complex thought in a succinct manner, and makes it possible to develop higher, even more complex thought. With the development of a general index notation for exponentiation, it becomes natural, for example, to refer to irrational powers of numbers. Consider, for example, the number (2^½)^(2^½), or √2^√2, a number now known to be transcendental; we no longer need a special word, as was the case prior to Wallis, to describe taking the √2-th power of another number, in this case the square root of 2.
In this post, I focused only on the introduction of index notation in The Arithmetic of the Infinitesimals. In the same book, in order to develop infinite series needed for the calculus, the continuous fraction notation was also developed. That will clearly require another post.
If you wish to donate to support my work, please use the Buy Me a Coffee app.
John Wallis. The Arithmetic of the Infinitesimals. Translated from Latin to English with an Introduction by Jacqueline A. Stedall. Springer, 2004.




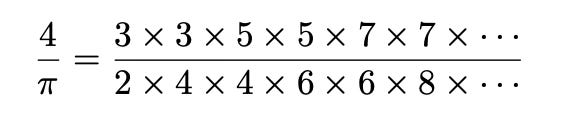



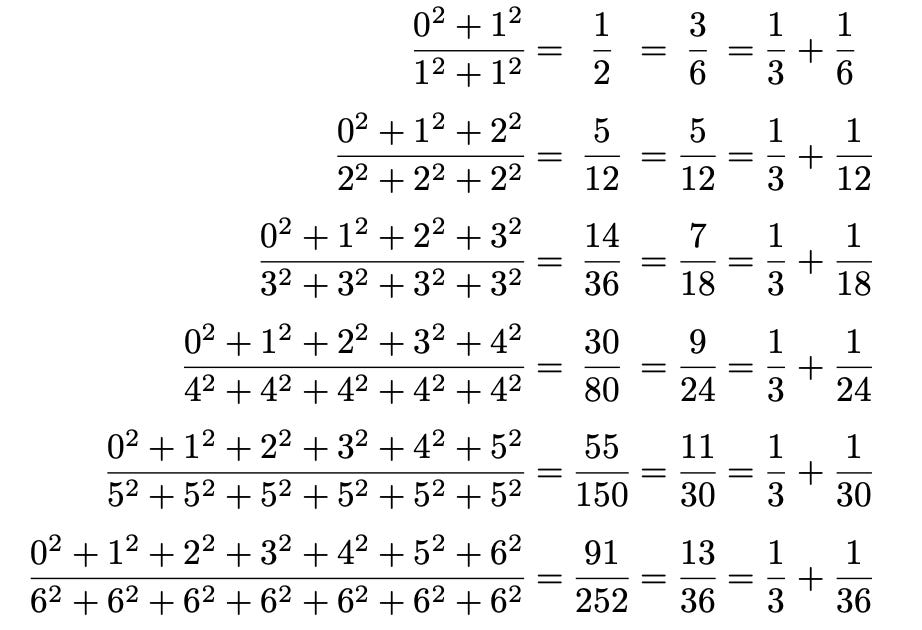
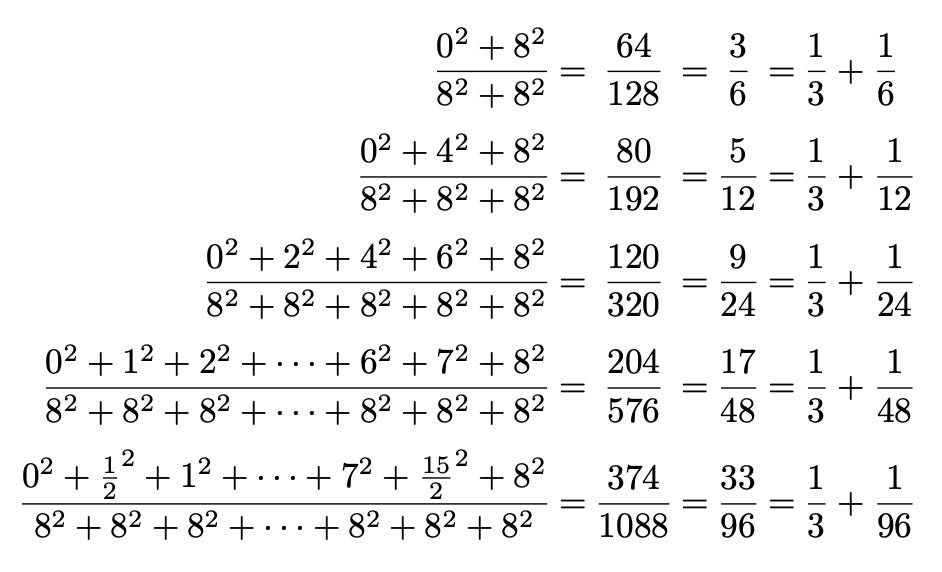

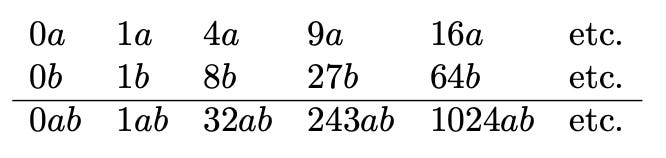
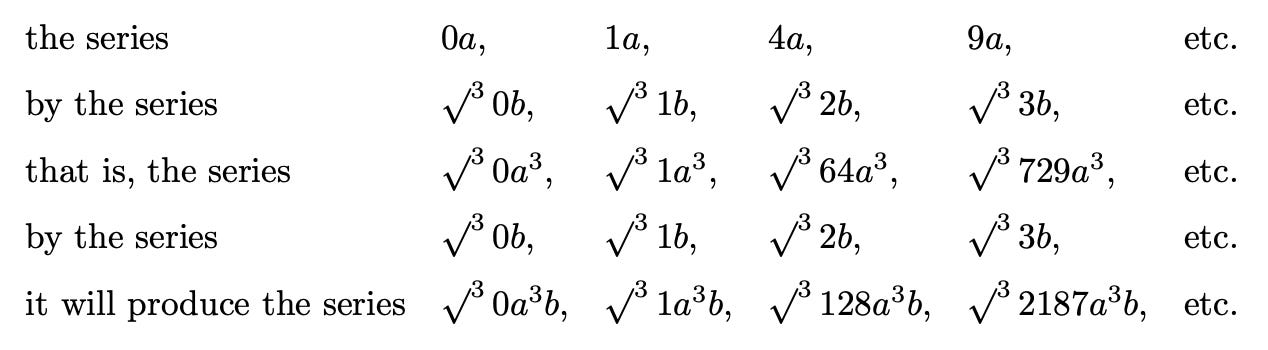
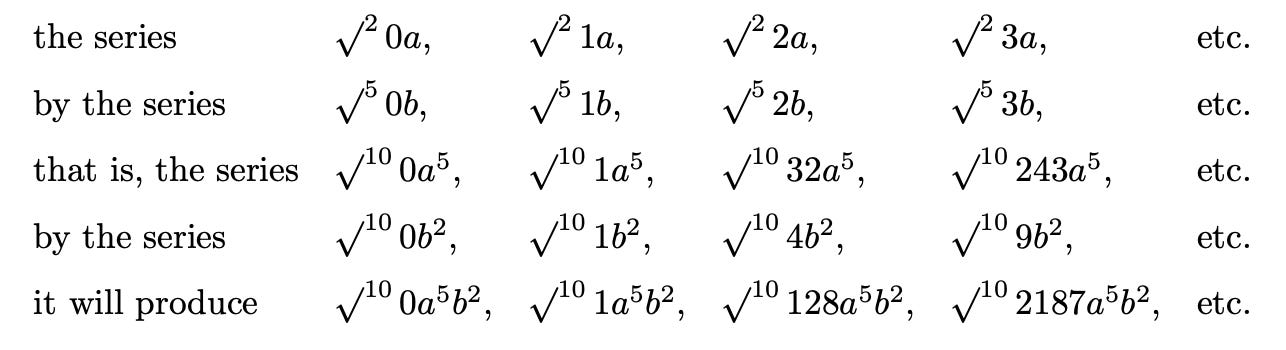
"Young man, in mathematics you don't understand things," said John von Neumann. "You just get used to them." You're showing that in the origin of these concepts, it was actually quite intuitive and reasonable.