In my earlier post The War Against the Infinitesimals, I examined the use of the infinitesimals by Leibniz and the subsequent response, often negative, thereto. But where did the term ‘infinitesimal’ come from?
In a letter to John Wallis (1616-1703), Gottfried Wilhelm Leibniz (1646-1716) wrote the following1:
for the calculus it is useful to imagine infinitely small quantities, or, as Nicolaus Mercator called them, infinitesimals.
Nicolaus Mercator [Nikolaus Kauffman] (1620-1687), is best known for his mathematical work Logarithmotechnia2, first published in 1667.
So I thought it would be interesting to find these references alluded to by Leibniz. Here is what I found. There are two occurrences of the word ‘infinitissimam’ in Mercator’s text:
in partem infinitissimam numeri dati [p.31]
in unam infinitissimam lineæ datæ [p.34]
Neither Google Translate nor Yandex Translate was capable of giving a reasonable translation, both rendering ‘infinitissiman’ into ‘infinite’. My translations are as follows:
in an infinitesimal part of the given number
in an infinitesimal of the given line
So here we see the word ‘infinitesimal’ used both as adjective and noun, as we would today in English.
Soon after, in an exchange3 with Wallis published in Philosophical Transactions, Mercator changes the spelling:
ubicunque, Lector offenderit infinitissimam, legar infinitesimam. [p.764]
My translation is as follows:
Wherever the reader may encounter the word infinitissimam, should be read infinitesimam.
So who was Nicholas Mercator? Josef Ehrenfried Hofmann (1900-1973), whom I quoted in my post, Joseph Ehrenfried Hofmann Demonstrates that Gottfried Wilhelm Leibniz Did Not Plagiarize Isaac Newton, writes4:
Mercator's life work is almost forgotten today, certainly unjustly. Mercator was a distinguished mathematician, physicist and astronomer. Shortly after his arrival in London the much-traveled man was received into the Royal Society. Products of that period are his new astronomical theory, the edition of Euclid, the navigation problems and the calculation of logarithms.
Hofmann gives a quick summary about Mercator’s use of infinite series:
In the third section the ordinate
of the equilateral hyperbola is transformed, by dividing out, into a power series. The surface of the hyperbola segment is built up entirely in the sense of Cavalieri’s method of infinitesimals [this is incorrect, Cavalieri worked with indivisibles] from the totality of all parallel coordinates “contained” in it. How one is to take and combine the sums over the single powers of x is only briefly alluded to. Thus Mercator gets the hyperbolic segment in that form which we would today write thus
However he does not express his result by a formula, but entirely in words. By means of an extremely bold conclusion he finds that this series can also be expressed by the logarithm of (1+x). The paper ends with the calculation of the body which "consists" of infinitely many hyperbolic segments. We would thus write the result expressed again only in words:
The latter equation, when the integration has been undertaken, gives what today is called Mercator’s series.
As for Leibniz, he writes5 about the importance of Mercator’s work:
Nicolaus Mercator Holsatus, Mathematicus et ipse praestantissimus, primus, quod sciam, quadraturam aliquam dedit per seriem infinitam. [p.232]
Here is an adapted Google translation:
Nicolaus Mercator of Holstein, a mathematician and himself the most eminent, was the first, as far as I know, to give any quadrature by an infinite series.
Mercator’s work, once published, did not go unnoticed. Wallis and Isaac Newton (1643-1727) were both working in a similar vein, but that will be the topic of future posts.
If you wish to donate to support my work, please use the Buy Me a Coffee app.
Letter to Wallis, 30 March 1699. In C.I. Gerhardt, (ed.): Leibnizens mathematische Schriften. Berlin and Halle: Eidmann, 1850-1863. Vol.IV, p.63. Quoted in translation in Mikhail G. Katz and David Sherry. Leibniz’s Infinitesimals: Their Fictionality, Their Modern Implementations, And Their Foes From Berkeley To Russell And Beyond. 2012. https://arxiv.org/abs/1205.0174v1
Nicolao Mercatore. Logarithmotechnia. Londini: Guilielmi Godbid, 1668.
M. Mercator. Some Illustration of the Logarithmotechnia. Philosophical Transactions 38:759-764, 1668.
Josef Ehrenfried Hofmann. On the Discovery of the Logarithmic Series and Its Development in England up to Cotes. National Mathematics Magazine 14(1):37-45.
De geometria recondita et analysi indivisibilium atque infinitorum. In C.I. Gerhardt (ed.): Leibnizens mathematische Schriften. Berlin and Halle: Eidmann, 1850-1863. Vol.I, pp.226-233.







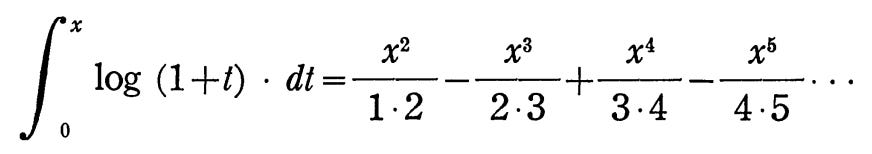
History of science/mathematics is so interesting. Glad to find your work. Thanks.